기존에 효과적인 Fine-Tuning 방법이라고만 대략적으로 알고 있었던 LoRA에 대해 자세하게 논문을 읽어보려 합니다.

최근에 NLP의 추세는 거대한 사전 학습 모델을 이용하여 여러 Down-Stream Task에 적용하는 것입니다. 보통은 기존 모델의 모든 파라미터를 Fine-Tuning을 이용하여 특정 작업에 효과적으로 만들고 있죠.

그런데 이를 몇몇 파라미터만을 적용하여 학습을 진행하거나, 외부 모델을 붙여 작업에 적용하는 방법으로 적용할 수 있다고 보았습니다. 현재까지 제시된 방법은 모델의 추론 속도를 늦추거나, 모델의 가용한 시퀀스 길이를 줄이는 효율과 성능의 Trade-Off 관계를 가집니다.

접근을 다르게 하여 작업에 비해 너무 많은 파라미터를 가진 모델은 실제로 낮은 Intrinsic Dimension을 가지고 있다는 발견을 기반으로 논문에서는 LoRA(Low-Rank Adaptation)을 제안합니다. LoRA는 사전 학습된 모델의 파라미터에 대해서는 고정을 시킨후 추가적인 파라미터를 통해 간접적으로 모델을 학습합니다.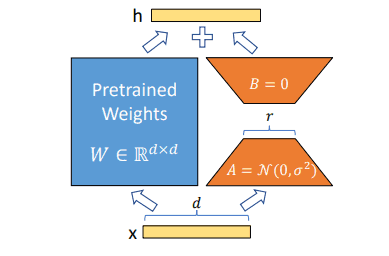

LoRA는 아래와 같은 이점이 있습니다.

Full Fine-Tuning 에서 업데이트되는 파라미터 $\Delta \Phi$의 크기는 기존 모델의 파라미터 $\Phi_0$와 같습니다. Fine-Tuning은 아래와 같은 Objective Function을 따르죠.

논문에서 제시하는 방법은 훨씬 적은 파라미터 $\Theta$에 대해 업데이트를 진행합니다. 학습되는 파라미터의 크기 $\Delta \Phi$는 $\Delta \Phi (\Theta)$와 같습니다. 이를 통해 Fine-Tuning을 진행하면 아래와 같은 Objective Function을 따르죠.

일반적으로 Full-Rank 행렬로 이루어져 있지만, 사전 학습된 언어 모델은 Low Instrisic Dimension을 가지고 더 적은 차원으로 효과적으로 학습시킬 수 있다고 가정합니다. 사전 학습 모델의 Weight $W_0 \in \mathbb{R}^{d \times k}$ 일때, $W_0$에 대해 업데이트를 진행하지 않습니다. 대신 새로운 Adapter $\Delta W$ 에 대해 업데이트를 진행하죠.

$A$와 $B$는 각각 학습 가능한 파라미터를 가지고 있습니다. 또한 $r$ 은 $d$와 $k$ 보다 훨씬 작은 차원을 가지도록 설정하여 낮은 Instrisic Dimension으로 연산을 수행할 수 있도록 하죠. 입력 $x$에 대한 $y$를 구하기 위해서는 아래와 같이 연산할 수 있습니다.

처음 파라미터를 초기화할 때 임의의 수로 $A$를, $B$는 모두 0으로 설정하여 $\Delta W = BA$ 는 0이 되도록 초기화합니다. 이후